Problemos ISSN 1392-1126 eISSN 2424-6158

2023, vol. 103, pp. 90–102 DOI: https://doi.org/10.15388/Problemos.2023.103.7

Educational Perspective: AI, Deep Learning, and Creativity

Augustinas Dainys
Vytauto Didžiojo universiteto Švietimo akademija
Email augustinas.dainys@vdu.lt
ORCID https://orcid.org/0000-0003-3905-4359

Linas Jašinauskas
Vytauto Didžiojo universiteto Švietimo akademija
Email linas.jasinauskas@vdu.lt
ORCID https://orcid.org/0000-0002-4968-412X

Abstract. Can artificial intelligence (AI) teach and learn more creatively than humans? The article analyses deep learning theory, which follows a deterministic model of learning, since every intellectual procedure of an artificial agent is supported by concrete neural connections in an artificial neural network. Meanwhile, human creative reasoning follows a non-deterministic model. The article analyses Bayes’ theorem, in which a reasoning system makes judgments about the probability of future events based on events that have happened to it. Meillassoux’s open probability and M. A. Boden’s three types of creativity are discussed. A comparison is made between the a priori algorithm of the Turing machine and a playing child, who invents new a posteriori algorithms while playing. The Heideggerian perspective on the co-creativity of humans and thinking machines is analyzed. The authors conclude that humans have an open horizon for teaching and learning, and that makes them superior with respect to creativity in an educational perspective.
Keywords: artificial intelligence, algorithm, Bayes’ theorem, open probability

Edukacinė perspektyva: dirbtinis intelektas, gilusis mokymasis ir kūrybiškumas

Santrauka. Straipsnyje analizuojama giliojo mokymosi teorija, kuri laikosi deterministinio mokymosi modelio, nes kiekviena dirbtinio agento intelektinė procedūra yra palaikoma konkrečių dirbtinio neuronų tinklo neuroninių jungčių. Jų yra labai daug, todėl imamas apibendrintas vidutinis vaizdas. O žmogaus kūrybinis mąstymas vadovaujasi nedeterministiniu modeliu. Straipsnyje analizuojama Bayeso teorema, pagal kurią mąstanti sistema, remdamasi jai nutikusiais įvykiais, daro išvadas apie būsimų įvykių tikimybę. Analizuojama Meillassoux atviroji tikimybė ir M. A. Boden trys kūrybiškumo tipai. Lyginamas apriorinis Turingo mašinos algoritmas ir žaidžiantis vaikas, kuris žaisdamas išranda naujus aposteriorinius algoritmus. Analizuojama heidegeriška abipusio kūrybingumo tarp žmogaus ir techninių mąstančių mašinų perspektyva. Daroma išvada, kad dirbtinis intelektas mokosi pagal užprogramuotą algoritmą, o žmogus turi atvirą mokymo ir mokymosi horizontą.
Pagrindiniai žodžiai: dirbtinis intelektas, algoritmas, Bayeso teorema, atviroji tikimybė

_________

Acknowledgment. We want to thank Prof. Aušra Saudargienė for her consultations and advice and for broadening our perspective in writing this article.

Received: 28/12/2022. Accepted: 30/03/2023
Copyright © Augustinas Dainys, Linas Jašinauskas, 2023. Published by Vilnius University Press.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (CC BY), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Introduction

To properly educate the younger generation is to have a real impact on society. Now, it can be seen that technologies change education and, in some way, that is changing humanity. How we educate the younger generation today affects the situation of society a few decades later, when the results of the educational efforts are manifest. Currently, studies of AI and digital technologies are very prolific, and there have been many discoveries in this field. In the eighteenth century, Watt first discovered the steam engine and that later provoked massive scientific investigation of thermodynamics. The recent rapid development of artificial intelligence (AI) has provoked reflection on the principles of AI. In this context, Anna Longo writes about the automation of philosophy and the subjugation of philosophizing to AI algorithms. She says “we are facing the affirmation of a universal automated method of knowledge production whose ambition is to provide the rules of inductive learning that can be applied to any discipline” (Longo 2021: 289-290). In the Middle Ages, philosophy was supposed to be the handmaiden of theology, and in the near future it is assumed it will become the handmaiden of AI, of intelligent and thinking machines, and justify a new automated and algorithmic state of knowledge production.

Marius P. Šaulauskas published a series of articles (Šaulauskas 2000, 2003, 2011) discussing the state of the digital and information society, and outlining the main principles of the digitalized state. “We still lack,” he wrote, “a regular Copernican revolution à la Kant, i.e. ‘a critique of digitalized reason’, to respond to the setup of telematic coexistence and reveal the potential and limits of the cognitive powers of ‘digitalized pure reason’” (Šaulauskas 2011: 9–10). Today, after a few decades of rapid development of AI, we also need a “critique of AI”, describing the main principles of creativity and thinking on the part of artificial agents. In this article, we try to offer a small outline of that project.

Lilija Duoblienė, reflecting on the place of technologies in future schools in the year 2050, says: “Robotization, AI, and information technologies will probably dominate the future school. A teacher might be a person who can keep up with technologies and in that way help young people to achieve competence. But it is unlikely that teachers will be authorities of the kind we envisage in talking about the year 2025” (see Murauskaitė 2022). But this fundamental assumption leads to a reflection on the principles that underlie the foundations of AI creativity.

In this paper, the basic principles of AI creativity will be discussed and contrasted with the logic of human creativity, which is referred to as creative learning and creative teaching. Examination is made of how human creativity and the logic of AI creativity fit together and differ. Will AI indeed replace human creativity in the future? Will technical progress really make humans abandon or limit their creative vocation and go on sabbatical? Will the creativity of thinking machines be much more efficient than purely human creativity? It is argued here that human creativity cannot be replaced by the creativity of thinking machines.

Deterministic and anti-deterministic models of reality

In modern science, there are two opposing models for thinking about reality: deterministic and anti-deterministic. The first is the model of thermodynamics or statistical physics, which considers the motion of gas particles and assumes that there are exact movements of concrete particles of reality. They can be measured, but our ability to do so is limited. Therefore, human thinking about reality has a subjective probabilistic nature. We take the average movements of gas particles, since we cannot objectively measure the exact movement of each particle, and say that it is probable that the state of the gas particles is now similar to this. However, if we had the needed equipment to measure the precise motion of each of the gas particles, we could describe that motion exactly. In this sense, nature is not playing dice and is the objective state of motion of the particles of nature, gas particles in this case.

The other model is that of quantum physics, which affirms objective probabilistic attitudes toward reality. This model is best described by Heisenberg’s uncertainty principle and the example of Schrӧdinger’s cat, where we cannot tell for sure whether it is alive or dead. It is impossible to describe the cat’s exact state, and such indetermination is considered an objective state of reality. In the quantum model, there is no such thing as an objective electron trajectory or history. We do not know its history, and that is the objective uncertainty inherent in reality; thus, it can be said that there is uncertainty in the structure of nature itself. It is a matter of the state of things, not of our subjective ignorance.

This paper reflects on the conflict between these two models, including the deterministic and the anti-deterministic educational perspectives. It is suggested that current AI technologies have shifted significantly toward the deterministic model. Theories of deep learning are being developed in an attempt to claim, in a similar way to the gas-particle model of thermodynamics or statistical physics, that there are concrete connections of artificial neurons in artificial neural networks, and they are objective. The various operations performed by AI are always based on precise connections of artificial neural networks, but one cannot think in detail about the connection parameters of each such connection. There are hundreds of billions of them, so thinking occurs in terms of common statistical states, much like the models of thermodynamics or statistical physics. Consider that the authors of one of the most prominent current books on deep learning theory, The Principles of Deep Learning Theory (Roberts, Yaida, Hanin 2022), wrote their dissertations on statistical physics. We argue that deterministic statistical physics could be rewritten in terms of deep learning theories, just replacing gas particles with artificial neural connections. It is thus assumed that determinism objectively exists, hence it is objectively possible to create an artificially creative learner.

Since there are so many artificial neuronal connections, one can only treat artificial neural communication networks probabilistically, theoretically, and say that a given input to an AI system yields a given output in the macro-phenomenological state of the artificial neural network system. The current state of science is such that a single artificial neural network can have approximately one hundred billion parameters (with more to come in the future). The main parameters are the threshold and the weighted connections between neurons, which are the basis for the function that describes the input, and after passing through the entire network of artificial neurons, provides the output. “[M]aking these adjustments to parameters is called training, and the particular procedure used to tune is called a learning algorithm” (Roberts, Yaida, Hanin 2022: 5).

Deterministic learning algorithms are strictly defined channel thresholds and weighted connections between neurons of artificial neural networks, which in our macroworld lead to different phenomenological AI activities and performances. AI robots perform different thinking operations processing the obtained data: a certain input gives a certain output. Following this logic, it can be said that AI systems are capable of deterministic learning and certain algorithms for learning systems are possible. If not yet fully known, this state of knowledge belongs to subjective probability and is a state of subjective ignorance This is similar to how scientists used to speak about subjective probability in the case of thermodynamic models, where it is hard to talk about the movement of a certain gas particle because it is difficult to measure, but in any case such movement takes place.

For this paper, a deterministic learning model was contrasted with an anti-deterministic learning model. The Turing machine was contrasted with a playing child whose play is more similar to the models described in quantum physics, when there is an objective uncertainty to reality. In a child’s play, things show themselves, and the play cannot be reduced to strict objective deterministic algorithms of play. A child is essentially indeterminate; he or she can play indeterminately. Thus their state is essentially similar to that of the electron trajectory in quantum physics, which is at once both a wave and a particle whose exact determination one cannot know, just as it is not known how, for a playing child, a concrete input will lead to a concrete output.

Therefore, in speaking about education, we will deal with objective probability. If a particular input is put into an individual educational system, i.e., a student, there will be no strictly defined output. There is a certain undecidability in the process of education.

Bayesian education

Deep learning theory, in analyzing artificial neural networks, describes the microlevel of learning: how the weighted connections between artificial neurons are formed during learning. Bayes’ theorem describes the macrolevel of learning: how a learning entity learns from events that occur and therefore anticipates events in the future, interacting with events in society and the Universe.

Bayes’ theorem states that:

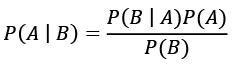
where: P is the probability; A is the Hypothesis of possible events; B is the event that increases or decreases the probability of Hypothesis A; P(A) is the a priori probability of Hypothesis A; P(B) is the probability of event B; P(B|A) is the conditional probability of event B under Hypothesis A; and P(A|B) is the a posteriori probability of Hypothesis A when B has occurred. Each system of Hypotheses A1, A2, ... is adjusted by newly occurring events B1, B2, ..., which change the reality of the existing Hypotheses A1, A2, ..., their status, either for or against, increasing or decreasing the likelihood of future probable events.

The Bayesian model is now being applied in the creation of AI, where each AI system has a given horizon of possibilities and acts according to various parameters, which depend on what happens. Each new event changes the state of the system itself because it already allows for some knowledge about the probabilities of future events, i.e., each new event changes our status as knowledgeable subjects so that there is a higher or lower probability of specific future events, depending on what has happened thus far. Bayes’ formula describes how AI learns, i.e., how it can react to events that have already happened and change its strategies for acting and predicting the future based on them.

Where is the problem? AI can outplay a chess grandmaster in a chess game. The Deep Blue computer won three games against world champion Garry Kasparov, for example. The problem, however, is that AI has an immediately given probability horizon. The Deep Blue chess-playing computer was given the eight-by-eight chessboard with 64 possible squares as 64 opportunities for the artificial chess player. AI cannot be a more creative learner than a human teacher or learner because it is given a closed total horizon, like the 8 × 8 chess grid. Learning does not just mean learning what is written in textbooks and mastering the possibilities they contain. It is also through free creative thinking that learners act and behave with an open horizon of probabilities. Bayes’ formula works even for the creative teacher and learner: each new event allows one to predict future events more accurately, thus accumulating experience. However, the horizon of the creative teacher’s and creative learner’s anticipation of future events is open. Human experience is essentially shaped by an open horizon of the future, and this is what distinguishes it from the experience of an AI, which is closed up in the algorithm of a probabilistic horizon. A creative teacher is not someone who knows all the possibilities of teaching in advance, but someone who responds to every Bayesian situation and makes decisions within an open horizon of future probabilities. In the case of AI, the horizon, as has already been said, is closed, defined by algorithms of what is expected.

Meillassoux probability

The French philosopher Quentin Meillassoux, in a chapter titled “Hume’s Problem” in his book After Finitude (Meillassoux 2008: 82-111), reframed the debate on probability. The term philosophical probability is used here to refer to Meillassoux’s probability. According to him, there is no immediately given horizon of probabilities in the Universe from which we must choose one as the probability of scoring the maximum number of points.

Suppose the probability of a result when throwing a dice can be calculated: where the dice has six sides, six probabilities, the probability of each result is one in six. However, Meillassoux, elaborating on Jean René Vernes’s critique of probabilistic reasoning, assumes “that these dice are not just six-sided but possess millions of millions of sides” (2008: 97). Disavowing mathematical probability opens an “acausal universe” (2008: 92), where a six-sided dice can turn into a million-faced dice, for example, and then back to a normal six-faced dice, again and again, later even becoming a billion-faced dice.

In this sense, the probability horizon from which to maximize one probability can be variable and indeterminate. That is why Meillassoux proposes thinking philosophically about a probability that does not have an immediately defined horizon of possibilities, when it is no longer known what to expect, because everything can happen. According to the now popular saying that accompanies Meillassoux’s philosophy, even if God has not existed up to now, there is a chance that He may begin to exist in the future. In this sense, anything can happen. The ordinary in our world can go from three-dimensional to three-thousand-dimensional, and there is no definite horizon of possibilities. This probability which occurs outside the horizon of probabilistic hypotheses is called a philosophical probability. It is a probability beyond what is expected from the world, while AI is based on a horizon of possibilities already given by a programmer. To put it in everyday terms, the calculation of probabilities by an AI from an already given horizon is an artisanal probability. A craftsman produces things according to a preexisting algorithm.

Definitions of a creative learner and a creative teacher

From discussion of Meillassoux’s philosophical probability, we move on to the definition of a creative learner and a creative teacher. We will refer to Meillassoux’s philosophical probability as the creator’s probability, and more specifically as the creative learner’s and the creative teacher’s probability. Although they may use a certain amount of deduction of prior probabilities from a context of already existing probabilistic possibilities, unlike an AI, the creative learner and teacher act in an open probability horizon. If an AI gets stuck when input data goes beyond its available algorithm, then, unlike AI, creative learners and teachers do not get stuck but find a creative way out of the situation, since they use intuition and creative thinking to find solutions to the most difficult situations. We will discuss this in more detail later in a later section, where Gӧdel’s incompleteness theorem is considered. Thus, AI will find such situations, which requires non-algorithmic creativity, to be unsolvable. But a creative learner or teacher in the same situation can go beyond all the algorithms that existed before and find a creative solution. This solution will be unlike the craftsman’s solution, which is made according to a certain algorithm. A creative solution goes beyond all the knowledge that was available before, finding some new and unexpected solution which was not predicted by all the probability prediction algorithms available. Therefore, AI cannot replace human creativity. As creative activities are not tied to any algorithms, their results go beyond the realms of algorithmically conditional possibilities.

Now, taking a closer look at the creative learner, the following situation is quite possible: in the course of education, a creative learner may ask a question that goes beyond the scope of the textbook and may be surprised by things that are not part of the textbook’s a priori knowledge. He or she may be surprised by what the teacher did not teach him. Or a teacher, in answering a creative learner’s question, and being creative, may go beyond what they learned at university or at doctoral level, and may spontaneously, creatively give interpretations that are not yet part of any teaching algorithm or universe of possibilities. In this sense, AI will never replace the creativity of the teacher. It works according to a given probability algorithm, while a creative teacher can create a new algorithm to answer a learner’s question. That is something AI is not able to do, in principle, if it is not programmed to do so. So, a creative question or answer is understood as one that goes beyond what is already possible. And, thus, a good description of a creative teacher or learner is a person who is not algorithm-minded.

Now, devoting a few sentences to the creator in general, a creator makes decisions and learns from current events in the context of an open horizon. Their solutions become creative because a creator goes beyond all previous algorithms and creates something that has never existed before. In this sense, they think in terms of Meillassoux’s philosophical probability, rather than in terms of models for existing solutions. A creator differs from a craftsman, who makes all solutions according to available algorithms. Whereas the creator, in creating, goes beyond the algorithms of all solutions that have existed before.

AI and the three types of creativity

Margaret A. Boden, in her article Creativity and AI¹(Boden 1998: 348), attempts to reflect on how AI can be creative. She distinguishes three types of creativity: 1) combinational creativity, where new ideas result from combining existing ideas; 2) exploratory creativity, where a certain conceptual territory is explored by walking around and looking at its particularity; and 3) transformational creativity, where existing givens of reality are transformed into new realities.

Boden concludes that AI most closely matches the exploratory type of creativity; it is most gifted at exploring varied conceptual, visual and sonic territories. She gives the example of music creation, where an AI is programmed with a certain musical grammar and a certain signature, as a musical coloring peculiarity, say to create music like Janis Joplin, for example. An AI can create music that fits all the stylistic and creative elements in Janis Joplin’s music on the basis of the grammatical principles and signatures summarized in it. Boden notes that an AI can create combinations of sounds that would be interesting for a professional musician to use in his or her creative work. Exploration takes place when musical grammar and signatures are given. Transformative creativity, the highest type, is where certain life events are transformed into a new reality and a work of literature or music is created unlike anything created before. AI can produce unique combinations of sounds and words and create music like that of Mozart or write poetry like Apollinaire’s. The problem is how to recognize those innovations.

Mathematically it is quite possible, if you put a monkey in front of a computer and it presses keys, and if you give it an infinite length of time, that the Iliad will be written. As Boden notes, however, creativity involves not only creating new and original combinations of signs but also distinguishing what has value from what does not. A monkey might write the Iliad, but, without understanding the worth of what it has done, it might then burn or erase it as completely worthless information. Creativity is therefore not only the ability to produce radical novelty but also the ability to recognize and select the unique meaningful combinations.

Viewing the rapid development of AI in the world today, it is recognized that AI can paint like van Gogh, make music like Mozart, and write poetry like Apollinaire. But for this, it is always given a musical or literary grammar. It is programmed with signatures and grammars as a kind of algorithms. The problem is whether AI can offer something completely new and original that has never existed in the history of culture. Such creativity would already be transformative – where the creator is inspired by the things of the world, but transforms, remakes, recreates them into something that has never existed before. As Boden points out, it is essential here to be able to discern and select what is truly original, because originality, as has already been said, can also be produced by a monkey. So whereas a computer can demonstrate the second, exploratory, type of creativity – writing according to Apollinaire’s grammar and style, but whether it is able to create as a completely new author or composer whose creations have value like the music of Mozart does is an open question.

As for the working hypothesis, then, given grammar and signatures as closed probabilistic horizons, a computer can indeed vary and create combinations that are interesting to professional creators and that they can use in their work. Can, however, an AI invent something it is not programmed for, something completely new, in the sense not of the second but of the third type of creativity? That is still an open question. Transformative creativity, which takes a detail of reality and transforms it into a whole new creative world that no one has thought about before and that is not defined by any algorithm that has existed until now, is unique to human creativity.

A Turing machine versus a playing child

In this section, a Turing machine and a playing child are compared, contrasting the model of algorithmic derivation against free play with reality’s particulars in which things crystallize. Western philosophy has been dominated by a desire to prove knowledge absolutely and to say strictly what propositions are false and what are true. For example, Leibniz developed the characteristica universalis, a language in which everything is calculated in order to determine whether particular statements are true or false. This line of thinking culminated in Russell’s and Whitehead’s Principia Mathematica, which applied Russell’s theory of types in trying to solve the liar’s paradox to find the absolute grounds of mathematics. Gödel, however, in his 1931 paper “On formally undecidable propositions of Principia Mathematica and related systems I”, discovered that, in any sufficiently rich system of knowledge, there will always be statements that are neither proven nor refuted, meaning that all sufficiently rich knowledge systems are incomplete. This criticism offered by Gödel was a critique of Western culture’s and philosophy’s search for absolute knowledge.

Then, five years later, in 1936, Alan Turing, in his article “On Computable Numbers, with an Application to the Entscheidungsproblem”, attempted to construct a logic machine to conceptualize algorithmic derivation. This project, in its own way, tried to restore the Leibnizian characteristica universalis project for the construction of a logic machine by admitting that there are also propositions which are neither provable nor disprovable. Turing, like Gödel, calls them undecidable statements, but there should be some rationally constructible part of knowing about which one can say with certainty whether these propositions are true or false. Turing asks what computable numbers are, and says that “a number is computable if its decimal can be written down by a machine” (Turing 2004: 58). This means that we have an algorithm or finite mean, i.e., a logical machine, to construct a computable number by a set of finite operations. An algorithm cannot operate infinitely; it gives a computable number which is rationally constructable in finite time by means of finite operations. Thus, in 1936, the idea of AI was born in an attempt to create a system where we could use a finite number of operations to rationally determine what statements are true and what are false. According to Turing, this system requires to count all the countable numbers in a finite number of operations where a computer can perform a finite number of finite operations in a finite amount of time. This domain of rational operations would be a Turing, or logical, machine.

As already mentioned, a Turing machine is an attempt to conceptualize an algorithm – to create a rational system in which some statements can be logically derived from others. The logical machine works on the principle that what is given now is the result of the prior state, and the present state determines the future state. A logical machine derives one statement from another statement, and yet another from that one, and such a derivation rule is an algorithm (although the meaning of algorithm is broader than a mere logical derivation, since an algorithm is a path from one proposition or state to another proposition or state).

On the other hand, Turing did not disprove Gödel’s incompleteness theorem, and Turing’s system contains unresolvable statements. Suppose a computer which encounters an unresolvable statement freezes and is unable to generate either ‘true’ or ‘false’ results. Viruses work similarly; they ‘short-circuit’ a logic machine by introducing self-referential states, like those that Russell attempted to resolve in his theory of types. Thus, it can be said that Gödel’s theorem shows the human mind cannot be reduced to a machine. In a sense, it outgrows it because a machine can only work according to programmed algorithms, and when it encounters something that is not in its algorithm, it gets stuck. Then, there is room for human creativity to come into play when a human tries to solve a problem where no algorithm can tell them what to do. So the machine works according to what is put into it, i.e., how it is programmed, whereas the human being, through creative thinking, can find a way out of an unsolvable problem. The problem of creativity arises in a situation of incomplete or unsolvable knowledge, where a new proposition cannot be logically derived from a previous proposition and the problem needs to be solved in a creative way to arrive at the next correct proposition. This is where the need for a creative solution comes in.

According to Šaulauskas, playing is inherent in the structure of the information society. So, the information society as a contemporary form of coexistence does not abolish homo ludens, which gave birth to all forms of culture, but even enhances it. “As our native language [Lithuanian] helpfully hints, the term ‘talk’ [žosmė], an articulated voice, comes directly from ‘play’ [žaismas], like a live and unplanned puzzle. May that unfettered puzzle begin with a primal utterance, i.e., with a promise to be awakened to oneself and others in all one says and hears. Because play, like speech, is ex definitio something communal – perhaps that is best and most succinctly expressed by the well-known concept of language-games that Ludwig Wittgenstein coined well before the dawn of the ‘information age’ ” (Šaulauskas 2011: 13). Thus, the information society does not abolish play but puts it at the center of its own existence.

Playing is also the most inherent state of a child’s existence and coexistence. A child’s state is absolutely creative. Hence, adults playing as children and with children learn to deal with situations creatively and to reject the algorithmic, mechanical social behavior that we have been taught. The difference between a child and an adult is that an adult is accustomed to acting mechanically, according to certain acquired algorithms, whereas the child has not learned many algorithms and so makes creative decisions in each case. That is why we want to contrast the playing child with a Turing logic machine which works mechanically, deriving one statement from another according to an algorithm. Meanwhile, the child plays creatively, and his or her game may include non-algorithmic solutions. The playing child discovers the algorithm in the game, while the Turing machine follows the algorithm it was designed to follow. In this sense, it is algorithmically probabilistic, because it has an algorithm that defines what to expect. Such an algorithm gives the logical machine a closed probability horizon, while the playing child operates with an open horizon of probabilities.

A priori and a posteriori algorithms

An AI is programmed to act and learn in a certain way. Its creator, the programmer, like God, creates an AI algorithm and programs it to perform some function, and the AI does that. It can even perform functions as complex as outplaying a chess grandmaster. However, as stated many times in this article, it operates within the horizon of possibilities that it has been given, while human creativity takes place within an open horizon of probabilities. Within the closed horizon of possibilities, an AI can be more powerful than a chess grandmaster because the grandmaster gets tired; the AI does not get tired and can play a very meticulous game of chess.

In comparing a child at play with an AI, our thesis is this: the child plays creatively. Undeniably, children’s play can follow different algorithms and there are different patterns in children’s development which educationalists study. Here we take play in the ideal sense, where the child in playing lets things occur, and not yet being trained to act in various defined ways, the child can play according to how things occur to them, not following way taught by kindergarten teachers and tutors. The child can therefore play creatively and be carried along in the game of things occurring. A child who plays does not have a preconceived algorithm for the game, so they play from the point of view of Meillassoux’s philosophical probability, where everything can happen. They do not have a closed horizon of possibilities. They do not get frustrated, as an adult might, that one thing is likely to happen and then this next thing is going to happen even though he or she prefers something else to happen.

The child playing is immersed in the game. Their algorithm is therefore developed through play, not pre-implanted by educators. The child, while playing, develops certain skills, like the ability to build play roads and make combinations of different words. As observation shows, the child does not follow a preconceived grammar of the Lithuanian or English (or any other) language or an algorithm of how Lithuanian or English should be spoken. He or she can make up words in a completely original way, or create unexpected combinations of words that are not proper Lithuanian or English. The child at play arranges words in their own way, and in this acts like a poet who discovers unexpected consonants in a language. All because, as noted above, the child does not have a pre-built or pre-trained algorithm. They create their own algorithms. That is why, in such a game, the algorithm always appears after the game, not before it as in the case of AI. While playing, the child may choose to play according to certain rules that have crystallized in the game and may invent some completely unexpected way of playing. Therefore, it is true that children also use rules when playing, but not the rules that adults taught them to follow, as is the case, for example, with AI, which follows the rules programmed by the programmer. The child, meanwhile, invents new rules for their game.

So, what makes a child’s play special is that the algorithm for the rules comes after the game. They do not go into the game with the algorithm. The child is therefore creative – not a craftsman who acts according to a preexisting model, but someone who invents new models and can incorporate them into his or her own and other children’s play activities. Even a philosopher can learn a lot from a child, and the practice of estrangement, when a philosopher learns to look at standard things in a nonstandard way, basically mimics child’s play. Inventors are special because they look at things from new perspectives, as if for the first time, with no preconceived algorithms, and then, after viewing things in this way, they let things show themselves and invent new algorithms of reality.

Heidegger, the question of technology and the problem of co-creativity

Heidegger thought about the Zusammengehörigkeit of being and the human being, i.e., about their fundamental relation, which is privileged. However, in the study The Question Concerning Technology, he also speaks about technology, which discloses physis and makes manifest the abilities of physis that are enclosed in natural beings. Therefore, there is a fundamental relation between physis and technology. Without technology, physis cannot be disclosed fully. In this relation, technology functions co-creatively with physis; creation discloses those characteristics of nature that, without creation, do not exist in a pure form.

Human beings also reveal their hidden abilities when they create a technical apparatus. Therefore, technology and humanity exist in a co-creative relationship. Technology also unveils secret abilities inherent in human nature, which, without technique, would not be made known. AI, too, discloses humans’ abilities, for example, by making their intellectual powers stronger. This is a co-creative relationship in which the deployment of human mental capacities is most fully disclosed by AI, and humanity obtains greater creative cognitive power than it would have without the technology of AI. This co-creative relationship is very important to us currently, as we live in an era of rapid development of AI. As we have shown, AI discloses human intelligence, and humanity is operating in a deep relationship with AI technologies, which involves the co-creation of the possibilities of the human physis.

Heidegger thought that human beings maintain their subjectivity and autonomy in relation to technology. The German philosopher thought that humans have a chance of co-creation in their relationship with technology. Heidegger did not, however, address AI or foresee its future possibilities. According to Anna Longo, it looks as though the following were true: 1) human beings are being reduced to the point where they will merely be a resource for AI; 2) thinking machines can fully simulate human capacities for learning; and 3) humans are historically predisposed to be subjugated to thinking machines as an object of their technical usage (Longo 2022: 14). In this discussion, we support the Heideggerian side, or at least we think that the question about human co-creative capacities with AI is still open.

Conclusion

It was shown that AI functions according to the algorithm for which it was programmed. It cannot go beyond this algorithm-encoded state, which creates a closed horizon of probabilities. One of the superiorities of AI is that it does not get tired in the course of its operations and does not make subjective mistakes. Unlike the human mind in, say, a chess game, An AI can outplay a chess grandmaster when the chess board is encoded as 8 × 8 possibilities.

A creative programmer can invent many AI algorithms, but a programmer can go beyond his or her own program which is coded for certain functions. Human creative learning and teaching go beyond these functions, and new algorithms can be invented through teaching and learning here and now. In contrast, AI is capable of inventing new algorithms only in keeping with the algorithm for which it is programmed to invent such algorithms. Therefore, AI cannot surpass human beings in learning and teaching creativity because it cannot go beyond the code that is given to it in the form of an algorithm. It can thus be concluded that AI will not surpass human creative powers in the future, even if it can play a better game of chess than a human being.

Hence, AI is not characterized by creative play, it is determined by algorithms. Creativity is closely linked to learning, and learning and teaching are undetermined processes.

AI is only effective within the boundaries set by the programmer. It may be more efficient than a human, as in the case of an artificial bus driver which can drive better than a human on certain routes but is completely inefficient beyond those limits. Meanwhile, human intelligence is much more versatile: it makes subjective mistakes when performing specific tasks but can discover areas that go beyond the limits of its initial learning.

Co-creativity of humans and AI is a tremendous historical chance for human beings to enter a new era of humanity and human evolution. Human beings obtain more intellectual powers, efficiency, and capabilities in co-creative co-existence with AI. Clearly, in the future many human functions will be transferred to thinking machines. This arrangement will have its benefits and its drawbacks. We can foresee that many human jobs will be lost due to technical progress.

References:

Boden, M. A., 1998. Creativity and AI. AI 103: 347–356.

Gödel, K., 1986. On formally undecidable propositions of Principia mathematica and related systems I. In: Collected Works, Volume I. Publications 1929–1936. Oxford, New York: Oxford University Press.

Heidegeris, M., 1992. Tecnikos klausimas. In Rinktiniai raštai. Vilnius: Mintis. Translated from German by A. Šliogeris: 217–243.

Longo, A., 2021. The Automation of Philosophy or the Game of Induction. Philosophy Today 65: 286–303.

Longo, A., 2022. Le jeu de l’induction: Automatisation de la connaissance et réflexion philosophique. Paris: Éditions mimésis.

Meillassoux, Q., 2008. After Finitude. An essay on the Necessity of Contingency. London, New Yourk: Continuum.

Mitchell, M., 2019. AI: A Guide for Thinking Humans. London: Pelican Books.

Murauskaitė, A., 2022. Kokia bus mokykla 2050 metais: mokytojus pakeis hologramos, formuosis socialiniai burbulai, trauksis lietuvių kalba? Prieiga per internetą: https://www.lrt.lt/naujienos/lietuvoje/2/1814738/kokia-bus-mokykla-2050-metais-mokytojus-pakeis-hologramos-formuosis-socialiniai-burbulai-trauksis-lietuviu-kalba [seen 28 Dec 2022]

Roberts, D. A., Yaida Sh. Hanin, B., 2022. The Principles of Deep Learning Theory. An Effective Theory Approach to Understanding Neural Networks. Cambridge: Cambridge University Press.

Šaulauskas, M. P., 2000. Metodologiniai informacijos visuomenės studijų profiliai: vynas jaunas, vynmaišiai seni? Problemos 58: 15–22.

Šaulauskas, M. P., 2003. Informacijos visuomenės samprata: senųjų vynmaišių gniaužtai. Problemos 64: 64–73.

Šaulauskas, M. P., 2011. Homo Irretitus: Politicus, Faber, Ludens. Sociologija. Mintis ir veiksmas 29: 5–15.

Turing, A., 2004. The Essential Turing. Seminal Writings in Computing, Logic, Philosophy, AI, and Artificial Life plus The Secrets of Enigma, ed. B. Jack Copeland. Oxford: Clarendon Press.

Wittgenstein, L., 1986. Philosophical Investigations. Oxford: Basil Blackwell.