Ekonomika ISSN 1392-1258 eISSN 2424-6166

2024, vol. 103(4), pp. 61–80 DOI: https://doi.org/10.15388/Ekon.2024.103.4.4

Fragile Union: A Machine Learning Analysis of Structural Heterogeneity and Divergence within the EMU

León Padilla*
Universidad de las Américas, Ecuador
Email: leon.padilla@udla.edu.ec 
ORCID: https://orcid.org/0000-0001-9455-0158

Sarah J. Carrington 
Pontificia Universidad Católica del Ecuador
Email: sjcarring@gmail.com
ORCID: https://orcid.org/0000-0002-9260-5028 

Eduardo Marín 
Tary Analytics, Madrid, Spain
Email: eduardo@tary.io

Abstract. This paper applies unsupervised machine-learning techniques to a set of nominal and industrial sector production variables to examine the convergence of European Monetary Union (EMU) member countries, focusing on macroeconomic and structural homogeneity. Our findings reveal distinct clusters of countries based on macroeconomic stability and industrial sector characteristics, highlighting a central group of core Northern European countries and a secondary group of peripheral, mainly Southern European economies. The significant differences between these clusters, particularly when considering real factors, underscore the fragility of the EMU in the face of large or asymmetric shocks. The study emphasized the need for structural reforms and careful analysis of economic characteristics to mitigate potential risks associated with expansion, ensuring the long-term stability and resilience of the union.
Keywords: Optimum currency areas, Monetary unions, Eurozone, Cluster analysis.

_________

* Correspondent author.
Received: 12/07/2024. Revised: 20/08/2024. Accepted: 26/10/2024
Copyright © 2024 León Padilla, Sarah J. Carrington, Eduardo Marín. Published by Vilnius University Press
This is an Open Access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

_________

1. Introduction

After a prolonged period of economic integration in Europe, the euro was introduced in January 2002. Initially, the founding countries of the eurozone included eleven member states: Germany, Austria, Belgium, Spain, Finland, France, Ireland, Italy, Luxembourg, the Netherlands, and Portugal. Over the following years, nine additional countries adopted the euro: Greece, Slovenia, Cyprus, Malta, Slovakia, Estonia, Latvia, Lithuania, and Croatia. The euro has effectively acted as a constant force for deepening and broadening European integration since the early 2000s. However, the euro crisis has called into question the integrity of the Eurozone, whose structural and institutional fault lines have been revealed by the financial crisis (Pegkas et al., 2020).

While there have been challenges concerning the monetary union in Europe, its formation was initially intended to foster economic prosperity by enhancing currency stability, reducing transaction costs, and promoting trade integration, while also curbing competitive devaluations (Covi, 2021; Frieden, 2002; Glick and Rose, 2016), fostering political integration to strengthen the European (Sadeh and Verdun, 2009; Van Oudenaren, 2005), facilitating financial market integration to enhance efficiency and competition (Stavarek et al., 2011), and promoting sustainable fiscal policy to reduce the risk of sovereign debt escalation (Allard et al., 2013; McNamara, 1999).

Many potential benefits of monetary unification depend on the similarities of member states’ economic structures, macroeconomic objectives, and the correlation of external shocks they face (Eichengreen, 1997). This research employs unsupervised machine learning techniques to assess the degree of similarity in economic dynamics among union member economies. While prior studies using cluster methodology focused on nominal variables based on Optimal Currency Area (OCA) theory and Maastricht Treaty criteria, this analysis incorporates additional industrial variables to capture the real economic structure. McKinnon (1963) and Kenen (1969) emphasize the crucial role of industrial similarities in forming a successful monetary union.

Unlike previous research that relies on simple averages of each variable to form clusters (Bénassy-Quéré and Coupet, 2005; Issiaka and Gnimassoun, 2013; Tsangarides and Qureshi, 2008), we enhance our approach by incorporating additional time series components, creating a comprehensive cross-sectional dataset for each set of indicators. For each country and series of indicators, we calculate the mean, standard deviation, and linear trend (linear regression slope). These metrics are employed in our clustering algorithms to assess EU member convergence in both real and nominal terms.

The paper is structured as follows. Section 2 presents a literature review of OCA theory. Section 3 explains the clustering methodology employed, while Section 4 elucidates the data utilized. Section 5 delineates the preliminary findings and the results of the cluster analysis. Section 6 presents a brief discussion of the policy implications of the study. The final section concludes.

2. Theoretical framework and Eurozone construction

The development of monetary union theory has been strongly influenced by both theoretical and practical perspectives, notably from the European Union’s experience. Mundell (1961) proposed the idea of a monetary area, defined either as a region using a single currency or as regions maintaining separate currencies but with fixed exchange rates. He argued that in the face of asymmetric demand shocks, factor mobility – particularly labor mobility – could act as an adjustment tool to offset the absence of independent monetary policy. McKinnon (1963) argued that both geographic and industrial labor mobility could help mitigate the effects of demand shocks. Kenen (1969) added that intra-industry mobility requires a high level of similarity in worker qualifications and economic characteristics. Additionally, economic openness supports the use of fixed exchange rates as the optimal currency system, while product diversification reduces the need for frequent trade and exchange rate adjustments.

Adopting a single currency offers both advantages and disadvantages. As noted by De Grauwe (2022), Hafner (2024), and Beck and Okhrimenko (2024), the primary costs include losing control over national monetary and exchange rate policies, which limits the ability to manage interest rates, money supply, and fiscal deficits. On the other hand, the benefits include fostering intraregional trade by lowering transaction costs and eliminating exchange rate risks, leading to welfare gains from reduced uncertainty and enhanced currency credibility.

To optimize the benefits of a European monetary union, the Maastricht Treaty established technical criteria for integration, focusing on “nominal” convergence. These conditions included limits on inflation, interest rates, fiscal deficits, public debt, and exchange rate policy (Kopits, 2002). Specifically, 1) inflation rates couldn’t exceed by more than 1.5% the average of the three EU countries with the lowest inflation, 2) long-term interest rates couldn’t exceed the same average by more than 2%, 3) no currency devaluations were allowed before joining the EMU, 4) the budget deficit had to stay under 3% of GDP, 5) and public debt had to be below 60% of GDP. Although these criteria aimed to align key macroeconomic indicators and ensure stability, they omitted important aspects from OCA theory, like industrial cohesion and synchronized economic cycles.

The focus on nominal convergence, however, proved to bring about limitations in Eurozone sustainability. Essentially, the emphasis on fiscal and monetary stability, without promoting real convergence through industrial cohesion, created vulnerabilities. Despite the initial success of the euro, where macroeconomic shocks appeared to converge (Coco and Silvestrini, 2017), the lack of real structural reforms exposed the union to significant risks.

During its first decade, the euro’s success may have fostered an illusion of deeper convergence. As Coco and Silvestrini (2017) showed, initially, macroeconomic shocks increased their comovement and decreased their size and persistence in eurozone countries compared with the UK and Sweden. However, economic activity, fueled by capital inflows, merely appeared to stimulate sustainable growth. This growth was debt-driven, lacking a corresponding increase in production capacity, leading to asset overvaluation and financial sector fragility (Coudert et al., 2020). The 2009 crisis exposed this fragility, resulting in sharp asset price falls, repressed economic activity, and a consequent spillover to public deficit and debt accumulation.

Following the 2009 financial crisis, economic shocks have become larger and more persistent on average (Coco and Silvestrini, 2017). Moreover, Ahmed et al. (2018) found evidence of business cycle decoupling in peripheral European countries relative to the core economies. This divergence was confirmed by Coudert et al. (2020), who identified distinct clusters of economies, with central countries like Belgium, France, Germany, Ireland, and the Netherlands forming one group, and peripheral countries like Austria, Finland, Spain, Italy, Portugal, and Greece forming another. Conforming the lack of convergence, Beck and Okhrimenko (2024) found that between 2006 to 2020, there was no club convergence for countries in terms of core–periphery or rich–poor regions.

Such unsynchronized macroeconomic fluctuations, combined with the loss of domestic monetary sovereignty, have materialized in persistent fiscal challenges. Effectively, without monetary policy as a tool for macroeconomic stability, countries have relied heavily on fiscal interventions, creating pressures on economies experiencing demand shocks out of sync with core countries. This divergence has widened the gap between core and peripheral countries, ultimately threatening the sustainability of the European Monetary Union.

3. Methodology

Cluster analysis is a fundamental method to investigate underlying dataset patterns (Yang and Hussain, 2023). Its primary function involves segmenting a dataset into clusters characterized by their internal similarities (Jain and Dubes, 1988). Operating within the statistical multivariate analysis realm (Kaufman and Rousseeuw, 1990), clustering represents an unsupervised learning technique employing pattern recognition and machine learning (Yang et al., 2018). Recent studies conducted for Africa (Bénassy-Quéré and Coupet, 2005; Issiaka and Gnimassoun, 2013; Tsangarides and Qureshi, 2008) and South America (Padilla and Marín, 2022) have employed various methods to identify candidates sharing similar economic characteristics and meeting the criteria necessary for common currency adoption. For this research, we applied standard clustering methods: (i) K-means clustering, (ii) the Partitioning Around Medoids (PAM) algorithm, (iii) Fuzzy C-Means clustering, and (iv) Agglomerative Hierarchical Clustering.

K-means clustering, proposed by MacQueen (1967) and improved by Hartigan and Wong (1979), aims to minimize intracluster variance by calculating the sum of squared Euclidean distances between centroids and observations. The algorithm starts by randomly assigning observations to clusters, calculates centroids, and iteratively assigns each data point to the nearest cluster until a stable solution is achieved. Due to its random initialization, multiple simulations are performed to find the optimal solution. Despite the need for extensive optimization, K-means remains the most widely used clustering algorithm due to its conceptual simplicity, ease of implementation, and versatility (Ashabi et al., 2021; Celebi et al., 2013).

One issue with K-means clustering is its sensitivity to outliers. K-medoid clustering offers an alternative by using representative objects called medoids instead of centroids (Park and Jun, 2009). Among K-medoids algorithms, PAM, proposed by Kaufman and Rousseeuw (1990), is considered highly effective. PAM is a partitioning clustering algorithm that aims to minimize the average dissimilarity between objects and their medoid in each cluster (Li et al., 2017). By minimizing distances to the closest medoid, PAM achieves two main benefits: a) it helps in splitting large clusters, ensuring elements are closer to their medoid, and b) it reduces the impact of outliers, as they have minimal effect on the distance sum (Van der Laan et al., 2003).

Unlike hard clustering algorithms like K-means, which strictly partition data points into distinct clusters, the Fuzzy C-Means (FCM) algorithm allows each data point to belong to multiple clusters with varying degrees of membership (Bezdek, 1973; Li et al., 2017). FCM weights centroids based on the degree of membership, inversely related to the distance from the cluster center. FCM is valued for its simplicity, ease of implementation, ability to handle large datasets, and robustness against outliers. The advantages of FCM include its simplicity, ease of implementation, ability to handle larger datasets, and robustness against outliers. In this study, the maximum belonging probability was considered when assigning a country to one of the obtained clusters.

Agglomerative Hierarchical Clustering (AHC) represents an alternative approach to partitioning algorithms. According to Nielsen (2016), hierarchical clustering involves constructing a binary merge tree (called a dendrogram), beginning with the data elements stored at the leaves, which are interpreted as singleton sets. The process continues by iteratively merging pairs of “closest” subsets, stored at nodes, until reaching the root of the tree, which contains all the dataset elements. From a dendrogram, multiple dataset partitions corresponding to flat clustering output can be extracted. The distance between any two subsets of the dataset is referred to as the linkage distance function. To select the most suitable linkage function for the data, the Cophenetic Coefficient (Sokal and Rohlf, 1962) was computed.

Regarding the validity of the clustering methodology, several works have recently been conducted on convergence between EU countries. Irac & Lopez (2015) identified two groups of countries within the original 12-nation euro area: one group comprising Greece, Italy, Portugal, and Spain, known as the southern countries, and another group consisting of the remaining countries. Casagrande & Dallago (2024) found that, despite the European integration process, the gap between northwestern and southeastern European countries has widened. (Coudert et al., 2020) used hierarchical ascendant classification (HAC) and factor analyses to identify two distinct groups of countries leading up to the EMU, with increasing differences between them. Their findings highlight the growing macroeconomic imbalances within the eurozone before the 2008 crisis and the subsequent fragmentation among its member countries. Using a fuzzy clustering technique, Ahlborn & Wortmann (2018) validate the presence of a stable core cluster, distinct from the clusters in Eastern and Southern European peripheries. Their findings also reveal that, following the financial crisis, the southern periphery exhibited divergent trends, while the eastern periphery showed signs of convergence. Finally, through k-means procedure and hierarchical cluster analysis, Amado (2023) found five clusters in Europe, with a clustering pattern between central and peripheral countries.

4. Data and variables

In this research, we include 28 European countries (27 member countries of the European Union and the United Kingdom). We do not include other European countries due to a lack of data availability. We utilize two sets of annual nominal and industrial time series indicators spanning from 2001 to 2019. The objective is to assess the degree of similarity among European countries based on the criteria for establishing a monetary area. Nominal indicators comprise seven variables pertinent to OCA theory and the criteria outlined in the Maastricht Treaty: inflation rates, fiscal balances, debt levels, interest rates, nominal exchange rate variability, intensity of regional trade, and labor market flexibility. The objective of clustering these variables is to facilitate assessing nominal convergence among the European countries. Following the approach highlighted by McKinnon (1963) and Kenen (1969), underscoring the importance of industrial similarities in forming a monetary union, we also incorporate industrial indicators to examine the degree of industrial similarities among European countries. The industrial indicators relate to the real sector and encompass seven variables: innovation, market size, competitiveness, real effective exchange rate fluctuation, productivity growth, industrial energy consumption, and market concentration.

Table 1 delineates the data sources, frequency, and imputation strategies applied to each variable. To address incomplete time series, we utilized three distinct imputation methods. Prior to 2006, the earliest available value in the series was used to impute missing values, while for the years 2007 to 2015, the mean was employed. For missing values in 2019, forecasts were generated using seasonal autoregressive integrated moving average (SARIMA) models. Notably, SARIMA models account for seasonal effects and are specifically designed for time series data, offering a robust framework (Divisekara et al., 2020).

Table 1. Data sources and periodicity

Note: * The imputation method used was SARIMA.

Conventional clustering algorithms typically necessitate cross-sectional data for training. Consequently, time series components were extracted from both nominal and industrial series to construct a unified cross-sectional dataset for each set of indicators.
Therefore, for every country and series in each set of indicators, the mean (mean), volatility (denoted by the standard deviation) (sd), and the linear trend (slp) (calculated as the slope of a linear regression on the indicator with time as the independent variable) were computed. Correlations (corr) were also computed among the annual GDP cyclical components (1960–2019) for each country and three main global economies (USA, EU, and China). These correlations were then integrated into each cross-sectional dataset. To obtain the cyclical components of annual GDP, the Baxter–King filter was used. Lastly, an automated variable selection procedure was conducted on each cross-sectional dataset to mitigate skewed clustering outcomes resulting from highly correlated variables (Sambandam, 2003). That is, the variables that showed very strong correlation were excluded. We opted for a threshold of |0.75|, representing a moderate/very strong threshold within the range of strong correlations (Akoglu, 2018).

5. Results

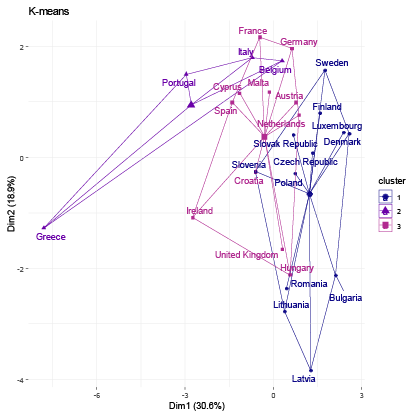
The resultant groups in the study were established using distinct criteria for each clustering method employed. To identify the optimal number of clusters for each algorithm, we calculated the Gap Statistic, as proposed by (Tibshirani et al., 2001). For hierarchical clustering, we calculated the Cophenetic Coefficient (Sokal and Rohlf, 1962) for Single, Complete, Average, and Ward linkage functions to determine the optimal linkage function (see Table 2). Average linkage achieved the highest Cophenetic Coefficient values of 0.679 and 0.647 for nominal and industrial variable sets, respectively, and was consequently selected for the analysis. For fuzzy clustering, the coefficients representing the probability of belonging to each cluster are provided in Table 3. We allocated each country to the cluster exhibiting the maximum probability. To determine the optimal number of clusters that best fit the data, we iteratively computed the GAP statistic for each clustering algorithm and dataset. The resulting GAP statistic values and the corresponding number of clusters are presented in Table 4. We include graphs 1–8 to portray the results for each method. The summary of the results is also presented in Tables 5 and 6.

Table 2. Cophenetic coefficient by clustering method for EU

Note: *Best linkage function.

Source: Author’s calculations.

Table 3. Fuzzy clustering – Probability of belonging to the EU

Note: The coefficients of belongingness of the country to each cluster.

Source: Author’s calculations.

Table 4. Gap Statistic and the optimal number of clusters for SA

Source: Author’s calculations.

Regarding the nominal indicators, the results show a coincidence of grouping for the countries that have generally experienced greater macroeconomic stability within the EU. Within this group of countries, the majority belong to the central nucleus of the EU (known as EU-12) and, in addition, the majority belong to the Eurozone. We identified two groups of countries that make up the same cluster despite different algorithms: Group 1 (Austria, Germany, Malta, and the Netherlands) and Group 2 (Bulgaria, Latvia, and Romania). These results are expected; however, they allow us to validate that the methodology used in this research produces results in line with other studies. For example, Gräbner et al. (2020a) develop a taxonomy of European economies that consists of four groups: Core (with Austria, Belgium, Denmark, Finland, Germany, and Sweden); Periphery (with Cyprus, France, Greece, Italy, Portugal, and Spain); Catch-Up (with Bulgaria, Romania, Czech Republic, Estonia, Latvia, Lithuania, Hungary, Poland, Slovenia, Slovakia); and Finance (Luxembourg, Netherlands, Malta, and Ireland). Borsi and Metiu (2015) identified “convergence clubs” in the EU. Their results suggest a clear separation between the new and old EU member states in the long run and a division along the South-East vs. North-West dimension since the 1990s. Finally, Erhart (2022) found that Austria, Finland, Denmark, Sweden, and Germany exhibited the highest level of adherence to the various criteria for the euro area in 2018, whereas Greece, Cyprus, Romania, Spain, and Italy demonstrated the lowest levels of compliance.

Regarding the industrial indicators, the results validating the method used are also encouraging. Austria, Belgium, Denmark, Germany, and Luxembourg, industrially developed countries, share the same cluster regardless of the algorithm used. Additionally, countries on the periphery of the EU are generally members of the same group (Greece, Ireland, Portugal, Spain, Italy). On the other hand, some small economies that have recently joined the EU also generally share the same group. One group includes Bulgaria, Croatia, Cyprus, and Malta, while another, the Republic of Slovakia, Romania, Lithuania, Latvia, and Poland.

These results corroborate other research. A recent study investigating whether economic integration within the EU has caused countries’ productive structures and sector-level productivity to converge over the period 1995–2018, found three “convergence clubs” as a result (Cavallaro and Villani, 2021). Club 1 is formed by Ireland, Luxembourg, Belgium, Denmark, France, and Germany; Club 2 is composed of the Netherlands, Austria, Finland, Italy, Spain, Sweden, United Kingdom, Slovenia, Lithuania, Poland, and Romania; Club 3 is formed by Croatia, Cyprus, Czechia, Estonia, Greece, Hungary, Latvia, Portugal, and Slovakia. In conclusion, the results of the methods applied for the EU favor the validation of the methodology used.

Table 5. Clustering methods summary for EU: nominal variables

Note: *Country is the center of the cluster (medoid). Countries in bold are currently part of the Eurozone.

Source: Author’s calculations.

Table 6. Clustering methods summary for EU: industrial variables

Note: *Country is the center of the cluster (medoid). Countries in bold are currently part of the Eurozone.

Source: Author’s calculations.

Figure 1. K-means for EU: nominal variables

Figure 2. K-medoids for EU: nominal variables

Figure 3. Hierarchical Average linkage for EU: nominal variables

Figure 4. Fuzzy clustering for EU: nominal variables

Figure 5. K-means for EU: industrial variables

Figure 6. K-medoids for EU: industrial variables

Figure 7. Hierarchical Average Linkage for EU: industrial variables

Figure 8. Fuzzy Clustering for EU: industrial variables

6. Policy implications

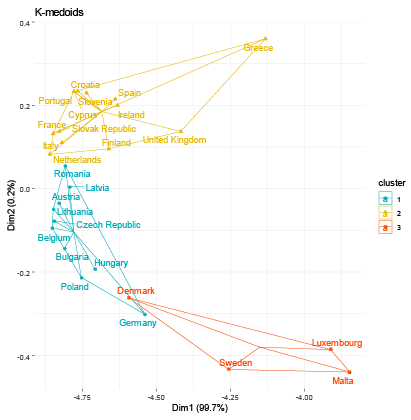
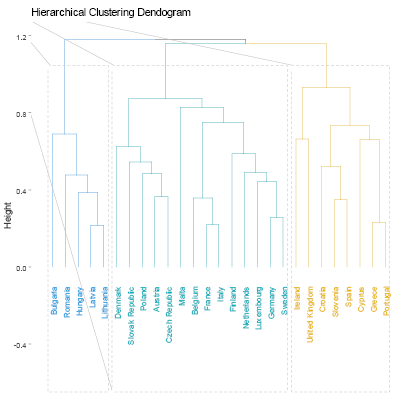
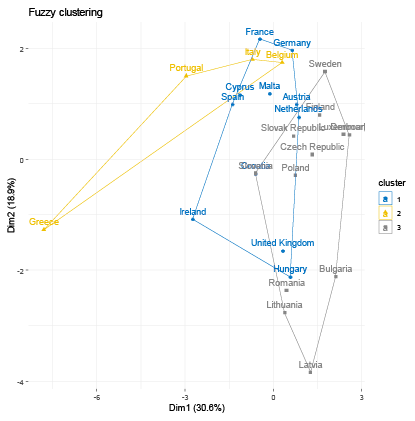
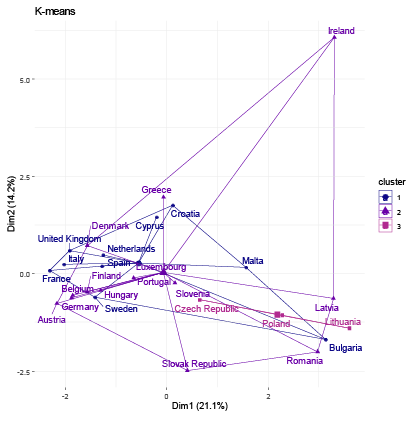
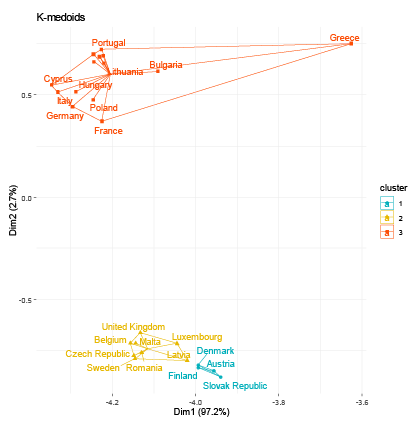
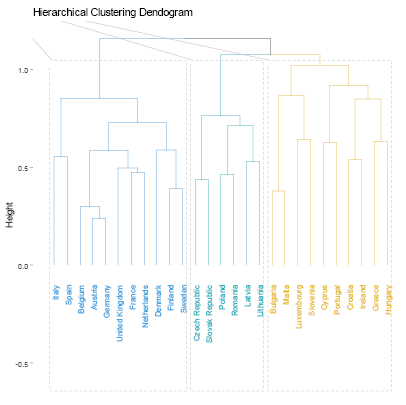
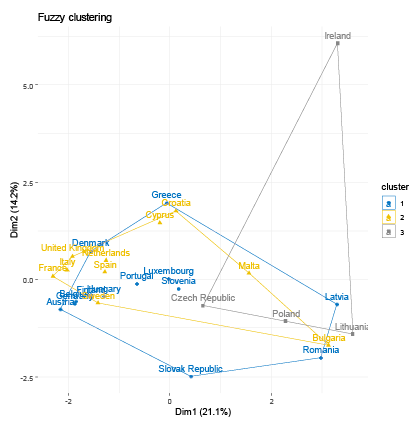
The EMU’s emphasis on nominal convergence for membership has obscured real outcome divergences (Franks et al., 2018). Our results corroborate other authors who suggest that divergence stems from the structural heterogeneity or “polarization” of its members (Gräbner et al., 2020b). That is, there are structural, commercial, and technological disparities among members. Core countries experience export-driven growth, while the peripheric economies rely on debt-driven growth, and lack the productivity increases to support this. Differences in market structures and income distributions between factor inputs further exacerbate the challenge of promoting convergence (Covi, 2021). In this context, achieving real economic convergence requires more than focusing on nominal macroeconomic indicators and fiscal and monetary stability.

As discussed in Section 2, the loss of monetary sovereignty and the need for macroeconomic stability in a monetary union like the EMU necessitate compensatory mechanisms. However, with fiscal policy constrained by Union rules, the burden of adjustment for countries experiencing asymmetric shocks falls on the real sector. According to the OCA literature, policy options to address this emphasize minimizing asymmetric economic shocks among currency union members to reduce reliance on secondary adjustment mechanisms. Yet even simultaneous shocks can lead to polarized economic performance when structural heterogeneity exists. Differences in production composition, market structures, regulatory frameworks, input factor use, and value chain networks mean that identical shocks can have varying impacts. Recovery speeds also differ, leading to groups of countries converging to different steady states (Monfort et al., 2013).

Thus, sustaining a balanced and functional OCA over time is a significant policy challenge, often requiring member states to make politically unpalatable economic adjustments. These costs increase with greater member heterogeneity. According to Kim (2024), the euro area’s fiscal crisis could have been resolved more swiftly and with less financial cost if fiscal risk-sharing mechanisms had been in place. These mechanisms would have produced economic effects similar to those of the flexible exchange rate system that existed before the adoption of the euro. While the response to the COVID-19 crisis was more equitable than that of the 2009 crisis, due to a more flexible institutional architecture, the EU is still not crisis-proof (De Angelis, 2022). To mitigate future risks, measures should be taken to avoid individualistic exit strategies from collective shocks. Additionally, careful consideration is needed when expanding the Eurozone to include structurally different countries with regulatory disparities. Prospective and current EMU members should evaluate their cluster positions and prioritize structural reforms to align with the Eurozone (Monfort et al., 2013).

7. Concluding remarks

In a monetary union, domestic priorities in monetary policy, exchange rate management, and fiscal policy are often subordinated to regional priorities, leaving countries with a more limited toolkit to address national challenges. This constraint becomes more pronounced with greater structural heterogeneity among economies and higher asymmetry in economic shocks. In this context, this paper has built on previous studies of the EMU by undertaking cluster analysis using machine-learning techniques and incorporating not just nominal variables, but also real variables.

The clustering analysis of EU countries based on both nominal and real (industrial) variables reveals distinct patterns and highlights critical differences between the two approaches. Nominal clustering consistently groups core EU countries like Germany, France, and the Netherlands, reflecting their macroeconomic stability and central role within the EU. Peripheral and emerging economies, such as Bulgaria, Romania, and Latvia, tend to cluster together, indicating shared economic challenges and lower stability levels. Greece frequently emerges as a distinct outlier in nominal clustering, underscoring its unique macroeconomic issues, particularly related to debt and fiscal stability.

In contrast, real clustering, which focuses on industrial variables, results in different groupings and highlights the importance of industrial structures over purely macroeconomic factors. While core countries remain grouped together, there are notable shifts, with countries like Ireland emerging as outliers due to their distinct industrial profiles, particularly their strong focus on high-tech industries and foreign investment. The real clusters also show more fluidity, especially in fuzzy clustering, where countries exhibit partial membership in multiple clusters, reflecting the complexity and interconnectedness of industrial economies.

These differences emphasize that while nominal variables provide insights into economic stability and integration, real variables offer a deeper understanding of industrial development and economic resilience. The results underscore the necessity of considering both perspectives to capture the full spectrum of economic and industrial dynamics within the EU, as they highlight different aspects of convergence and divergence among member states.

Our methodology thus yields results that generally align with previous studies but highlight that nominal and real variables cluster slightly differently. The divergence between clusters suggests increasing potential costs and reduced benefits of union membership over time. The 2009 Euro-crisis exposed fragility in the EMU, and it appears that insufficient progress has been made to address this issue. Real convergence is crucial for the sustainability of integration over time. As Europe expands EMU membership, this paper emphasizes the necessity of careful analyzing new members’ suitability. Future structural reforms and a thorough analysis of economic characteristics to mitigate potential risks associated with expansion are needed to ensure the long-term stability and resilience of the union.

References

Ahlborn, M., Wortmann, M., 2018. The core‒periphery pattern of European business cycles: A fuzzy clustering approach. J Macroecon 55, 12–27. https://doi.org/https://doi.org/10.1016/j.jmacro.2017.08.002

Ahmed, J., Chaudhry, S.M., Straetmans, S., 2018. Business and Financial Cycles in the Eurozone: Synchronization or Decoupling. The Manchester School 86, 358–389. https://doi.org/https://doi.org/10.1111/manc.12188

Akoglu, H., 2018. User’s guide to correlation coefficients. Turk J Emerg Med 18, 91–93. https://doi.org/https://doi.org/10.1016/j.tjem.2018.08.001

Allard, C., Brooks, P., Bluedorn, J., Bornhorst, F., Ohnsorge, F., Christopherson Puh, K., 2013. Toward A Fiscal Union for the Euro Area, IMF Staff Discussion Notes. International Monetary Fund.

Amado, G., 2023. Revisiting the debate on the Eurozone crisis: causes, clustering periphery and core, and the role of interest rate convergence. Int Rev Appl Econ 37, 642–666. https://doi.org/10.1080/02692171.2023.2240269

Ashabi, A., Sahibuddin, S. Bin, Salkhordeh Haghighi, M., 2021. The Systematic Review of K-Means Clustering Algorithm, in: Proceedings of the 2020 9th International Conference on Networks, Communication and Computing, ICNCC ’20. Association for Computing Machinery, New York, NY, USA, pp. 13–18. https://doi.org/10.1145/3447654.3447657

Beck, K., Okhrimenko, I., 2024. Optimum Currency Area in the Eurozone. Open Economies Review. https://doi.org/10.1007/s11079-024-09750-z

Bénassy-Quéré, A., Coupet, M., 2005. On the adequacy of monetary arrangements in sub-Saharan Africa. World Economy 28, 349–373. https://doi.org/10.1111/j.1467-9701.2005.00649.x

Bezdek, J.C., 1973. Fuzzy mathematics in pattern classification.

Borsi, M.T., Metiu, N., 2015. The evolution of economic convergence in the European Union. Empir Econ 48, 657–681. https://doi.org/10.1007/s00181-014-0801-2

Casagrande, S., Dallago, B., 2024. Exploring Global Economy Evolution: Clusters and Patterns. Economies 12. https://doi.org/10.3390/economies12020032

Cavallaro, E., Villani, I., 2021. Club Convergence in EU Countries. Journal of Economic Integration 36, 125–161.

Celebi, M.E., Kingravi, H.A., Vela, P.A., 2013. A comparative study of efficient initialization methods for the k-means clustering algorithm. Expert Syst Appl 40, 200–210. https://doi.org/https://doi.org/10.1016/j.eswa.2012.07.021

Coco, A., Silvestrini, A., 2017. The nature and propagation of shocks in the euro area: A comparative SVAR analysis. International Journal of Computational Economics and Econometrics 7, 95–114. https://doi.org/10.1504/IJCEE.2017.080615

Coudert, V., Couharde, C., Grekou, C., Mignon, V., 2020. Heterogeneity within the euro area: New insights into an old story. Econ Model 90, 428–444. https://doi.org/https://doi.org/10.1016/j.econmod.2019.11.028

Covi, G., 2021. Trade imbalances within the Euro Area: two regions, two demand regimes. Empirica 48, 181–221. https://doi.org/10.1007/s10663-020-09477-3

De Angelis, G., 2022. COVID-19 Challenges to the European Economic and Monetary Union: Institutional Responses, Growth Strategies, and Future Prospects in a Changing Macroeconomic Environment—Introduction. International Journal of Political Economy 51, 2–4. https://doi.org/10.1080/08911916.2022.2048552

De Grauwe, P., 2022. Economics of the Monetary Union, 14th ed. Oxford University Press.

Divisekara, R.W., Jayasinghe, G.J.M.S.R., Kumari, K.W.S.N., 2020. Forecasting the red lentils commodity market price using SARIMA models. SN Business & Economics 1, 20. https://doi.org/10.1007/s43546-020-00020-x

Eichengreen, B., 1997. European monetary unification : theory, practice, and analysis. Cambridge, Mass., Cambridge, Mass.

Erhart, S., 2022. Ready or not? Constructing the Monetary Union Readiness Index. Journal of Central Banking Theory and Practice 11, 23–66. https://doi.org/doi:10.2478/jcbtp-2022-0002

Franks, J., Barkbu, B., Blavy, R., Oman, W., Schoelermann, H., 2018. Economic Convergence in the Euro Area: Coming Together or Drifting Apart? IMF Working Papers 18, 1. https://doi.org/10.5089/9781484338490.001

Frieden, J.A., 2002. Real Sources of European Currency Policy: Sectoral Interests and European Monetary Integration. Int Organ 56, 831–860. https://doi.org/DOI: 10.1162/002081802760403793

Glick, R., Rose, A.K., 2016. Currency unions and trade: A post-EMU reassessment. Eur Econ Rev 87, 78–91. https://doi.org/https://doi.org/10.1016/j.euroecorev.2016.03.010

Gräbner, C., Heimberger, P., Kapeller, J., Schütz, B., 2020a. Structural change in times of increasing openness: assessing path dependency in European economic integration. J Evol Econ 30, 1467–1495. https://doi.org/10.1007/s00191-019-00639-6

Gräbner, C., Heimberger, P., Kapeller, J., Schütz, B., 2020b. Is the Eurozone disintegrating? Macroeconomic divergence, structural polarisation, trade and fragility. Cambridge J Econ 44, 647–669. https://doi.org/10.1093/cje/bez059

Hafner, K.A., 2024. Monetary union in Southeast Asia: An assessment of the optimum currency area theory. World Econ 47, 2445–2475. https://doi.org/https://doi.org/10.1111/twec.13539

Hartigan, J.A., Wong, M.A., 1979. Algorithm AS 136: A K-Means Clustering Algorithm. J R Stat Soc Ser C Appl Stat 28, 100–108. https://doi.org/10.2307/2346830

Irac, D., Lopez, J., 2015. Euro area structural convergence? A multi-criterion cluster analysis. International Economics 143, 1–22. https://doi.org/https://doi.org/10.1016/j.inteco.2015.01.005

Issiaka, C., Gnimassoun, B., 2013. Optimality of a monetary union: New evidence from exchange rate misalignments in West Africa. Econ Model 32, 463–482. https://doi.org/10.1016/j.econmod.2013.02.038

Jain, A.K., Dubes, R.C., 1988. Algorithms for Clustering Data, Prentice Hall advanced reference series. Prentice Hall.

Kaufman, Leonard., Rousseeuw, P.J., 1990. Finding Groups in Data: An Introduction to Cluster Analysis (Wiley Series in Probability and Statistics), Eepe.Ethz.Ch. https://doi.org/10.1007/s13398-014-0173-7.2

Kenen, P., 1969. The Theory of Optimum Currency Areas: An Eclectic View, in: Mundell, R. and Swoboda., A. (Ed.), Monetary Problems of the International Economy. University of Chicago Press, Chicago, pp. 41–60.

Kim, W.-D., 2024. A study on a new fiscal risk-sharing system to make Eurozone an OCA. International Journal of Finance & Economics 29, 2415–2427. https://doi.org/https://doi.org/10.1002/ijfe.2790

Kopits, G., 2002. Central European EU accession and Latin American integration: Mutual lessons in macroeconomic policy design. North American Journal of Economics and Finance 13, 253–277. https://doi.org/10.1016/S1062-9408(02)00092-X

Li, Z., Wang, G., He, G., 2017. Milling tool wear state recognition based on partitioning around medoids (PAM) clustering. The International Journal of Advanced Manufacturing Technology 88, 1203–1213. https://doi.org/10.1007/s00170-016-8848-1

MacQueen, J., 1967. Some methods for classification and analysis of multivariate observations, in: Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics, Fifth Berkeley Symposium on Mathematical Statistics and Probability. University of California Press, Berkeley, Calif., pp. 281–297.

McKinnon, R.I., 1963. Optimum Currency Areas. Am Econ Rev 53, 717–725.

McNamara, K.R., 1999. The Currency of Ideas, Monetary Politics in the European Union. Cornell University Press. https://doi.org/doi:10.7591/9781501711930

Monfort, M., Cuestas, J.C., Ordóñez, J., 2013. Real convergence in Europe: A cluster analysis. Econ Model 33, 689–694. https://doi.org/https://doi.org/10.1016/j.econmod.2013.05.015

Mundell, R.A., 1961. A Theory of Optimum Currency Areas. The American Economic ReviewAmerican Economic Review 51, 657–665.

Nielsen, F., 2016. Hierarchical Clustering BT  - Introduction to HPC with MPI for Data Science, in: Nielsen, F. (Ed.), . Springer International Publishing, Cham, pp. 195–211. https://doi.org/10.1007/978-3-319-21903-5_8

Padilla, L., Marín, E., 2022. Monetary Integration in South America: Election of Candidates Through Unsupervised Machine Learning. Revista de Economía Mundial 63–89. https://doi.org/10.33776/rem.v0i61.5155

Park, H.-S., Jun, C.-H., 2009. A simple and fast algorithm for K-medoids clustering. Expert Syst Appl 36, 3336–3341. https://doi.org/https://doi.org/10.1016/j.eswa.2008.01.039

Pegkas, P., Staikouras, C., Tsamadias, C., 2020. On the determinants of economic growth: Empirical evidence from the Eurozone countries. International Area Studies Review 23, 210–229. https://doi.org/10.1177/2233865920912588

Sadeh, T., Verdun, A., 2009. Explaining Europe’s Monetary Union: A Survey of the Literature. International Studies Review 11, 277–301.

Sambandam, R., 2003. Cluster Analysis Gets Complicated. Marketing Research.

Sokal, R.R., Rohlf, F.J., 1962. The comparison of dendrograms by objective methods. Taxon. https://doi.org/10.2307/1217208

Stavarek, D., Repkova, I., Gajdosova, K., 2011. Theory of financial integration and achievements in the European Union, MPRA Paper. University Library of Munich, Germany. https://doi.org/DOI:

Tibshirani, R., Walther, G., Hastie, T., 2001. Estimating the number of clusters in a data set via the gap statistic. J R Stat Soc Series B Stat Methodol. https://doi.org/10.1111/1467-9868.00293

Tsangarides, C.G., Qureshi, M.S., 2008. Monetary Union Membership in West Africa: A Cluster Analysis. World Dev 36, 1261–1279. https://doi.org/10.1016/j.worlddev.2007.06.019

Van der Laan, M., Pollard, K., Bryan, J., 2003. A new partitioning around medoids algorithm. J Stat Comput Simul 73, 575–584. https://doi.org/10.1080/0094965031000136012

Van Oudenaren, J., 2005. Uniting Europe: an introduction to the European Union. Rowman & Littlefield.

Yang, M.-S., Chang-Chien, S.-J., Nataliani, Y., 2018. A Fully-Unsupervised Possibilistic C-Means Clustering Algorithm. IEEE Access PP, 1. https://doi.org/10.1109/ACCESS.2018.2884956

Yang, M.-S., Hussain, I., 2023. Unsupervised Multi-View K-Means Clustering Algorithm. IEEE Access 11, 13574–13593. https://doi.org/10.1109/ACCESS.2023.3243133